4.2 Context-Free Grammars

4.2.3 Derivations

NOTE: Derivation means 推导 in Chinese.

The construction of a parse tree can be made precise by taking a derivational view, in which productions are treated as rewriting rules. Beginning with the start symbol, each rewriting step replaces a nonterminal by the body of one of its productions. This derivational view corresponds to the top-down construction of a parse tree, but the precision afforded by derivations will be especially helpful when bottom-up parsing is discussed. As we shall see, bottom-up parsing is related to a class of derivations known as "rightmost" derivations, in which the rightmost nonterminal is rewritten at each step.

NOTE:

I still do not understand why bottom-up parsing corresponds "rightmost" derivations.

$\Rightarrow$

If $S \xrightarrow []{ \ast} \alpha$ where $S$ is the start symbol of a grammar $G$, we say that $\alpha$ is a sentential form of G. Note that a sentential form may contain both terminals and nonterminals, and may be empty. A sentence of G is a sentential form with no nonterminals. The language generated by a grammar is its set of sentences. Thus, a string of terminals $w$ is in $L(G)$, the language generated by G, if and only if $w$ is a sentence of G (or $S \xrightarrow []{ \ast} w $. A language that can be generated by a grammar is said to be a context-free language. If two grammars generate the same language, the grammars are said to be equivalent.

NOTE: Natural language is not context-free language.

To understand how parsers work, we shall consider derivations in which the nonterminal to be replaced at each step is chosen as follows:

1、In leftmost derivations, the leftmost nonterminal in each sentential is always chosen. If $\alpha \to \beta $ is a step in which the leftmost nonterminal in $\alpha$ is replaced, we write $\alpha \xrightarrow [ \text{lm} ]{} \beta$ .

2、In rightmost derivations, the rightmost nonterminal is always chosen; we write $\alpha \xrightarrow [ \text{rm} ]{} \beta$ in this case.

If , then we say that is a left-sentential form of the grammar at hand.

Analogous definitions hold for rightmost derivations. Rightmost derivations are sometimes called canonical derivations.

4.2.4 Parse Trees and Derivations

A parse tree is a graphical representation of a derivation that filters out the order in which productions are applied to replace nonterminals. Each interior node of a parse tree represents the application of a production. The interior node is labeled with the nonterminal A in the head of the production; the children of the node are labeled, from left to right, by the symbols in the body of the production by which this A was replaced during the derivation.

NOTE: Left-most derivation and right-most derivation yield the same tree in the end but the order in which productions are applied to replace nonterminals is different.

4.2.7 Context-Free Grammars Versus Regular Expressions

NOTE:

下面这些内容是在阅读 wikipedia Comparison of parser generators 中 Regular languages 章节时，发现这一段的内容正好和本节内容相关，可以作为一个补充，并且它的讲解也比较易懂：

Regular languages are a category of languages (sometimes termed Chomsky Type 3) which can be matched by a state machine (more specifically, by a deterministic finite automaton or a nondeterministic finite automaton) constructed from a regular expression. In particular, a regular language can match constructs like "A follows B", "Either A or B", "A, followed by zero or more instances of B", but cannot match constructs which require consistency between non-adjacent elements, such as "some instances of A followed by the same number of instances of B", and also cannot express the concept of recursive "nesting" ("every A is eventually followed by a matching B"). A classic example of a problem which a regular grammar cannot handle is the question of whether a given string contains correctly-nested parentheses. (This is typically handled by a Chomsky Type 2 grammar, also termed a context-free grammar.)

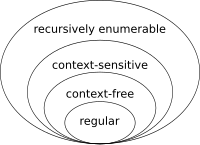
regular expression属于Regular languages，使用regular grammar，按照Chomsky hierarchy:

• regular grammar属于Type-3 grammars
• context-free grammar属于Type-2 grammars

Every regular language is context-free, every context-free language is context-sensitive, every context-sensitive language is recursive and every recursive language is recursively enumerable. These are all proper inclusions, meaning that there exist recursively enumerable languages that are not context-sensitive, context-sensitive languages that are not context-free and context-free languages that are not regular.