geeksforgeeks Expression Tree

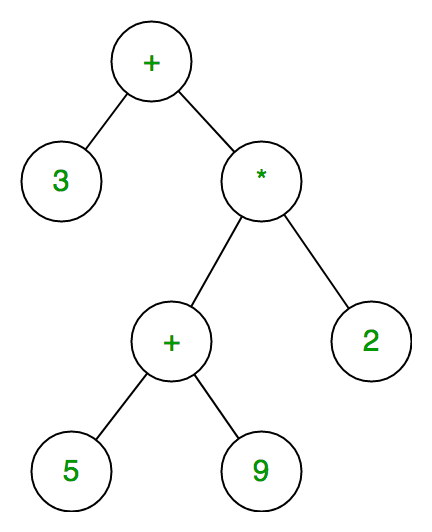
Expression tree is a binary tree in which each internal node corresponds to operator and each leaf node corresponds to operand so for example expression tree for 3 + ((5+9)*2) would be:

Inorder traversal of expression tree produces infix version of given postfix expression (same with preorder traversal it gives prefix expression)

Evaluating the expression represented by expression tree:

Let t be the expression tree
If  t is not null then
      If t.value is operand then  
                Return  t.value
      A = solve(t.left)
      B = solve(t.right)

      // calculate applies operator 't.value' 
      // on A and B, and returns value
      Return calculate(A, B, t.value)

NOTE:

典型的递归、自顶向下、binary tree-DFS-post order后序-return value

Construction of Expression Tree:

Now For constructing expression tree we use a stack. We loop through input expression and do following for every character.

1) If character is operand push that into stack

2) If character is operator pop two values from stack make them its child and push current node again.

At the end only element of stack will be root of expression tree.

// C++ program for expression tree
#include<bits/stdc++.h>
using namespace std;

// An expression tree node
struct et
{
    char value;
    et *left, *right;
};

// A utility function to check if 'c'
// is an operator
bool isOperator(char c)
{
    if (c == '+' || c == '-' || c == '*' || c == '/' || c == '^')
        return true;
    return false;
}

// Utility function to do inorder traversal
void inorder(et *t)
{
    if (t)
    {
        inorder(t->left);
        printf("%c ", t->value);
        inorder(t->right);
    }
}

// A utility function to create a new node
et* newNode(int v)
{
    et *temp = new et;
    temp->left = temp->right = NULL;
    temp->value = v;
    return temp;
}
;

// Returns root of constructed tree for given
// postfix expression
et* constructTree(char postfix[])
{
    stack<et*> st;
    et *t, *t1, *t2;

    // Traverse through every character of
    // input expression
    for (int i = 0; i < strlen(postfix); i++)
    {
        // If operand, simply push into stack
        if (!isOperator(postfix[i]))
        {
            t = newNode(postfix[i]);
            st.push(t);
        }
        else // operator
        {
            t = newNode(postfix[i]);

            // Pop two top nodes
            t1 = st.top(); // Store top
            st.pop();    // Remove top
            t2 = st.top();
            st.pop();

            // make them children
            t->right = t1;
            t->left = t2;

            // Add this subexpression to stack
            st.push(t);
        }
    }

    // only element will be root of expression
    // tree
    t = st.top();
    st.pop();

    return t;
}

// Driver program to test above
int main()
{
    char postfix[] = "ab+ef*g*-";
    et *r = constructTree(postfix);
    printf("infix expression is \n");
    inorder(r);
    return 0;
}
// g++ test.cpp --std=c++11 -pedantic -Wall -Wextra

NOTE:

自底向上，两两合并

Output:

infix expression is
a + b - e * f * g

This article is contributed by Utkarsh Trivedi. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.