Write a program to print all permutations of a given string

问题描述

A permutation, also called an “arrangement number” or “order,” is a rearrangement of the elements of an ordered list S into a one-to-one correspondence with S itself. A string of length n has n! permutation. Source: Mathword(http://mathworld.wolfram.com/Permutation.html)

Below are the permutations of string ABC. ABC ACB BAC BCA CBA CAB

算法

Here is a solution that is used as a basis in backtracking.

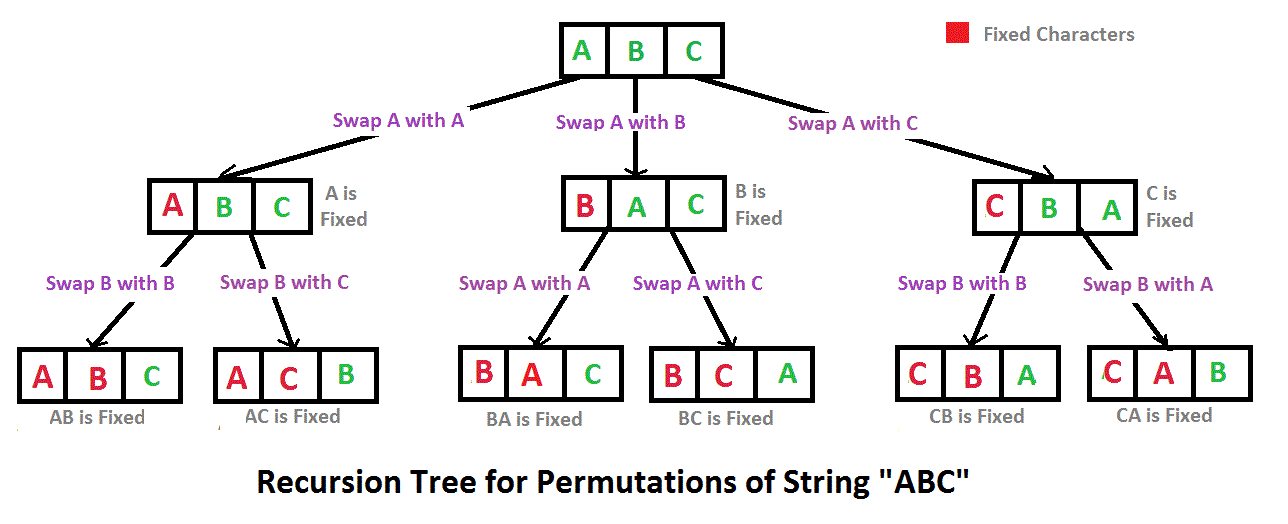
NewPermutation

SUMMARY : 上述图已经非常好地展示了backtracking算法的调用过程，结合下面的代码来看的话，对上面的recursion tree进行先序遍历就是下面的函数的调用过程；该函数的目的是生成所有的permutation的，即它需要穷举；

生成permutation的过程可以简述为：

从n个元素中挑选出一个来作为第0个元素
从n-1个元素中挑选出一个来作为第1个元素
从n-2个元素中挑选出一个来作为第2个元素
...
从2个元素中挑选出一个来作为第n-2个元素
从1个元素中挑选出一个来作为第n-1个元素

显然上述过程是一个递归的过程，上述过程如果使用图形化来展示的话，其实和上面的recursion tree是完美对应的：

recursion tree的第一层节点，对应了从n（n=3）个元素中挑选出一个来作为第0个元素
recursion tree的第二层节点，对应了从n-1（n-1=2）个元素中挑选出一个来作为第1个元素

recursion tree中的每一条路径就对应了一个组合；

所以，共有 $n \times (n-1) \times (n-2) \times \ldots \times 2 \times 1$ 种排列， $n \times (n-1) \times (n-2) \times \ldots \times 2 \times 1$ 是和上述recursion tree完美对应的:

第一个元素选定为A，对应了第一棵子树，显然共有n棵类似这样的子树，所以是 $n \times$

由于我们的backtrack算法目的是**穷举**，所以在第一个元素选定为A后，还需要去尝试第一个元素选定为B的情况，还需要去产生第一个元素选定为C的情况；以此类推，在第二个元素选定为A后，还需要去尝试第二个元素选定为B的情况，还需要去产生第二个元素选定为C的情况；所以我们需要回溯，即回退到上一层的状态，这样上一层就能够尝试另外一种情况了；其实这就是backtracking算法的核心思想所在了；

对上述递归数进行先序遍历就对应了递归函数实际的执行过程，需要注意的是，当第一次由上到下经过一条边的时候，执行swap函数，当第二次由下到上经过该边的时候，执行方向相反的swap函数；这也说明递归调用是深度优先地遍历。

那上述过程如何使用递归函数来进行实现呢？这就是一个程序员需要考虑的问题了。对于这个问题，我们常常考虑的是使用backtracking算法：

`C++`

// C++ program to print all 
// permutations with duplicates allowed 
#include <bits/stdc++.h> 
using namespace std; 


// Function to print permutations of string 
// This function takes three parameters: 
// 1. String 
// 2. Starting index of the string 
// 3. Ending index of the string. 
void permute(string a, int l, int r) 
{ 
    // Base case 
    if (l == r) 
        cout<<a<<endl; 
    else
    { 
        // Permutations made 
        for (int i = l; i <= r; i++) 
        { 

            // Swapping done 
            swap(a[l], a[i]); 

            // Recursion called 
            permute(a, l+1, r); 

            //backtrack 
            swap(a[l], a[i]); 
        } 
    } 
} 

// Driver Code 
int main() 
{ 
    string str = "ABC"; 
    int n = str.size(); 
    permute(str, 0, n-1); 
    return 0; 
} 

// This is code is contributed by rathbhupendra

C

// C program to print all permutations with duplicates allowed 
#include <stdio.h> 
#include <string.h> 

/* Function to swap values at two pointers */
void swap(char *x, char *y) 
{ 
    char temp; 
    temp = *x; 
    *x = *y; 
    *y = temp; 
} 

/* Function to print permutations of string 
This function takes three parameters: 
1. String 
2. Starting index of the string 
3. Ending index of the string. */
void permute(char *a, int l, int r) 
{ 
int i; 
if (l == r) 
    printf("%s\n", a); 
else
{ 
    for (i = l; i <= r; i++) 
    { 
        swap((a+l), (a+i)); 
        permute(a, l+1, r); 
        swap((a+l), (a+i)); //backtrack 
    } 
} 
} 

/* Driver program to test above functions */
int main() 
{ 
    char str[] = "ABC"; 
    int n = strlen(str); 
    permute(str, 0, n-1); 
    return 0; 
}