Graph、tree and list

进化：从list到tree，从tree到graph；

退化：graph退化为tree，tree退化为list；

树和图都可能退化成链，所以其实链也具备部分tree和graph的关系。反过来说其实就是树和图是链的泛化。

其实可以看到，很多基于graph、tree的结构或设计都有对应的线性版本，比如 Merkle tree，它的线性版本就是Hash chain。

从relation的角度来进行分析

参见 Relation-structure-computation\Model 章节。

freefeast Difference between Trees and Graphs | Trees vs. Graphs

	Trees	Graphs
Path	Tree is special form of graph i.e. minimally connected graph and having only one path between any two vertices.	In graph there can be more than one path i.e. graph can have uni-directional or bi-directional paths (edges) between nodes
Loops	Tree is a special case of graph having no loops, no circuits and no self-loops.	Graph can have loops, circuits as well as can have self-loops.
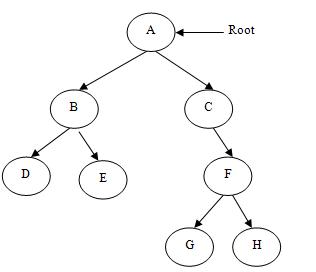
Root Node	In tree there is exactly one root node and every child have only one parent.	In graph there is no such concept of root node. NOTE: In graph, a node can be specified as the root node.
Parent Child relationship	In trees, there is parent child relationship so flow can be there with direction top to bottom or vice versa.	In Graph there is no such parent child relationship.
Complexity	Trees are less complex then graphs as having no cycles, no self-loops and still connected.	Graphs are more complex in compare to trees as it can have cycles, loops etc
Types of Traversal	Tree traversal is a kind of special case of traversal of graph. Tree is traversed in Pre-Order, In-Order and Post-Order (all three in DFS or in BFS algorithm)	Graph is traversed by DFS: Depth First Search and in BFS : Breadth First Search algorithm
Connection Rules	In trees, there are many rules / restrictions for making connections between nodes through edges.	In graphs no such rules/ restrictions are there for connecting the nodes through edges.
DAG	Trees come in the category of DAG : Directed Acyclic Graphs is a kind of directed graph that have no cycles.	Graph can be Cyclic or Acyclic.
Different Types	Different types of trees are : Binary Tree , Binary Search Tree, AVL tree, Heaps.	There are mainly two types of Graphs : Directed and Undirected graphs.
Applications	Tree applications : sorting and searching like Tree Traversal & Binary Search.	Graph applications : Coloring of maps, in OR (PERT & CPM), algorithms, Graph coloring, job scheduling, etc.
No. of edges	Tree always has n-1 edges.	In Graph, no. of edges depend on the graph.
Model	Tree is a hierarchical model.	Graph is a network model.
Figure

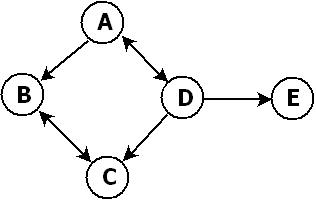树中每个节点都只能有一个父节点，图中一个节点可以有多个父节点。

离散数学中对tree的定义：

a tree is a connected undirected graph with no simple circuits

这蕴含着

an undirected graph is a tree if and only if there is a unique simple path between any two of its vertices

如果两个点之间有多条path的话，则必然就形成了circuit了