B-tree
Example
segmentfault 由 B-/B+树看 MySQL索引结构
cornell B-Trees
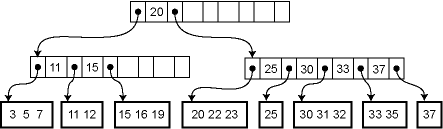
wikipedia B-tree
NOTE:
In computer science, a B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree is a generalization of a binary search tree in that a node can have more than two children.[1] Unlike other self-balancing binary search trees, the B-tree is well suited for storage systems that read and write relatively large blocks of data, such as discs(磁盘). It is commonly used in databases and file systems.
NOTE:
B-tree能够帮助快速地找到文件的位置
What, if anything, the B stands for has never been established.
Overview
In B-trees, internal (non-leaf) nodes can have a variable number of child nodes within some pre-defined range. When data is inserted or removed from a node, its number of child nodes changes. In order to maintain the pre-defined range, internal nodes may be joined or split. Because a range of child nodes is permitted, B-trees do not need re-balancing as frequently as other self-balancing search trees, but may waste some space, since nodes are not entirely full. The lower and upper bounds on the number of child nodes are typically fixed for a particular implementation. For example, in a 2-3 B-tree (often simply referred to as a 2-3 tree), each internal node may have only 2 or 3 child nodes.
NOTE:
一、join、split是在insert、delete 时经常发生的事情
二、B-tree的内部实现是以空间换时间
"Because a range of child nodes is permitted, B-trees do not need re-balancing as frequently as other self-balancing search trees, but may waste some space, since nodes are not entirely full."
三、在学习B-tree的时候,需要注意它的:
1、child node的个数、branch的个数、degree
2、separation key的个数
两者之间的关系为: N(child node ) = N(separation key) ;
2-3 B-tree 的"2-3"指的是child node的个数 ;
Each internal node of a B-tree contains a number of keys. The keys act as separation values which divide its subtrees. For example, if an internal node has 3 child nodes (or subtrees) then it must have 2 keys: *a*1 and *a*2. All values in the leftmost subtree will be less than *a*1, all values in the middle subtree will be between *a*1 and *a*2, and all values in the rightmost subtree will be greater than *a*2.
NOTE:
分段
Usually, the number of keys is chosen to vary between $ d $ and $ 2d $, where $ d $ is the minimum number of keys, and $ d+1 $ is the minimum degree or branching factor of the tree(d个数,可以将数轴分为d+1段).
NOTE:
这段话中的"the number of keys"指的是什么?指的是 "internal node of a B-tree"
In practice, the keys take up the most space in a node. The factor of 2 will guarantee that nodes can be split or combined(这段话中的2所指为前面的2d). If an internal node has $ 2d $ keys, then adding a key to that node can be accomplished by splitting the hypothetical(假设的) $ 2d+1 $ key node into two $ d $ key nodes and moving the key that would have been in the middle to the parent node. Each split node has the required minimum number of keys. Similarly, if an internal node and its neighbor each have $ d $ keys, then a key may be deleted from the internal node by combining it with its neighbor. Deleting the key would make the internal node have $ d-1 $ keys; joining the neighbor would add $ d $ keys plus one more key brought down from the neighbor's parent. The result is an entirely full node of $ 2d $ keys.
NOTE: : B-tree只有叶子节点才存储value;red-black tree的所有节点都存储值;skip list和B-tree比较类似,它的最底层才存储value
命名法
NOTE:
一、使用分支、子节点个数来进行命名
二、从前面的介绍可知: d 指的是 "$ d $ is the minimum number of keys"
The number of branches (or child nodes) from a node will be one more than the number of keys stored in the node. In a 2-3 B-tree, the internal nodes will store either one key (with two child nodes) or two keys (with three child nodes). A B-tree is sometimes described with the parameters $ (d+1) $ — $ (2d+1) $ or simply with the highest branching order, $ (2d+1) $.
Variants
The term B-tree may refer to a specific design or it may refer to a general class of designs. In the narrow sense, a B-tree stores keys in its internal nodes but need not store those keys in the records at the leaves. The general class includes variations such as the B+ tree and the B* tree.
1、In the B+ tree, copies of the keys are stored in the internal nodes; the keys and records are stored in leaves; in addition, a leaf node may include a pointer to the next leaf node to speed sequential access.
2、The B* tree balances more neighboring internal nodes to keep the internal nodes more densely packed.
3、B-trees can be turned into order statistic trees to allow rapid searches for the Nth record in key order, or counting the number of records between any two records, and various other related operations.
B-tree usage in databases
Time to search a sorted file
Usually, sorting and searching algorithms have been characterized by the number of comparison operations that must be performed using order notation. A binary search of a sorted table with N records, for example, can be done in roughly ⌈ log2 N ⌉ comparisons. If the table had 1,000,000 records, then a specific record could be located with at most 20 comparisons: ⌈ log2 (1,000,000) ⌉ = 20.
An index speeds the search
A significant improvement can be made with an index. In the example above, initial disk reads narrowed the search range by a factor of two. That can be improved substantially by creating an auxiliary index that contains the first record in each disk block (sometimes called a sparse index). This auxiliary index would be 1% of the size of the original database, but it can be searched more quickly. Finding an entry in the auxiliary index would tell us which block to search in the main database; after searching the auxiliary index, we would have to search only that one block of the main database—at a cost of one more disk read. The index would hold 10,000 entries, so it would take at most 14 comparisons. Like the main database, the last six or so comparisons in the auxiliary index would be on the same disk block. The index could be searched in about eight disk reads, and the desired record could be accessed in 9 disk reads.
Insertions and deletions
Advantages of B-tree usage for databases
The B-tree uses all of the ideas described above. In particular, a B-tree:
1、keeps keys in sorted order for sequential traversing
2、uses a hierarchical index to minimize the number of disk reads
3、uses partially full blocks to speed insertions and deletions
4、keeps the index balanced with a recursive algorithm
In addition, a B-tree minimizes waste by making sure the interior nodes are at least half full. A B-tree can handle an arbitrary number of insertions and deletions.
Technical description
Definition
According to Knuth's definition, a B-tree of order m is a tree which satisfies the following properties:
1、Every node has at most m children.
2、Every non-leaf node (except root) has at least ⌈m/2⌉ child nodes.
3、The root has at least two children if it is not a leaf node.
4、A non-leaf node with k children contains k − 1 keys.
5、All leaves appear in the same level and carry no information.
Each internal node’s keys act as separation values which divide its subtrees. For example, if an internal node has 3 child nodes (or subtrees) then it must have 2 keys: *a*1 and *a*2. All values in the leftmost subtree will be less than *a*1, all values in the middle subtree will be between *a*1 and *a*2, and all values in the rightmost subtree will be greater than *a*2.
Algorithms
NOTE:
一、主要是增删改查
