wisc Red-Black Trees

Introduction

Recall that, for binary search trees, although the average-case times for the lookup, insert, and delete methods are all O(log N), where N is the number of nodes in the tree, the worst-case time is O(N). We can guarantee O(log N) time for all three methods by using a balanced tree -- a tree that always has height O(log N)-- instead of a binary search tree.

A number of different balanced trees have been defined, including AVL trees, 2-4 trees, and B trees. You might learn about the first two in an algorithms class and the third in a database class. Here we will look at yet another kind of balanced tree called a red-black tree.

The important idea behind all of these trees is that the insert and delete operations may restructure the tree to keep it balanced. So lookup, insert, and delete will always be logarithmic in the number of nodes but insert and delete may be more complicated than for binary search trees.

A red-black tree is a binary search tree in which

一、each node has a color (red or black) associated with it (in addition to its key and left and right children)

二、the following 3 properties hold:

1、(root property) The root of the red-black tree is black

2、(red property) The children of a red node are black.

3、(black property) For each node with at least one null child, the number of black nodes on the path from the root to the null child is the same.

An example of a red-black tree is shown below:

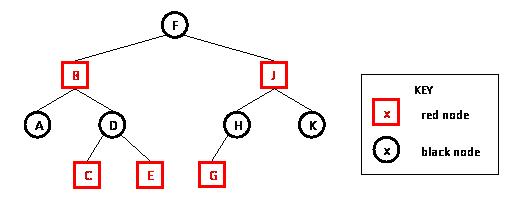
Operations on a Red-Black Tree

As with the binary search tree, we will want to be able to perform the following operations on red-black trees:

• insert a key value (insert)
• determine whether a key value is in the tree (lookup)
• remove key value from the tree (delete)
• print all of the key values in sorted order (print)

Because a red-black tree is a binary search tree and operations that don't change the structure of a tree won't affect whether the tree satisfies the red-black tree properties, the lookup and print operations are identical to lookup and print for binary search trees.

The insert operation

The goal of the insert operation is to insert key K into tree T, maintaining T's red-black tree properties. A special case is required for an empty tree. If T is empty, replace it with a single black node containing K. This ensures that the root property is satisfied.

If T is a non-empty tree, then we do the following:

1. use the BST insert algorithm to add K to the tree
2. color the node containing K red
3. restore red-black tree properties (if necessary)