geeksforgeeks Trie | (Insert and Search)

Trie is an efficient information re**Trie**val data structure. Using Trie, search complexities can be brought to optimal limit (key length). If we store keys in binary search tree, a well balanced BST will need time proportional to M * log N, where M is maximum string length and N is number of keys in tree. Using Trie, we can search the key in O(M) time. However the penalty is on Trie storage requirements (Please refer Applications of Trie for more details)

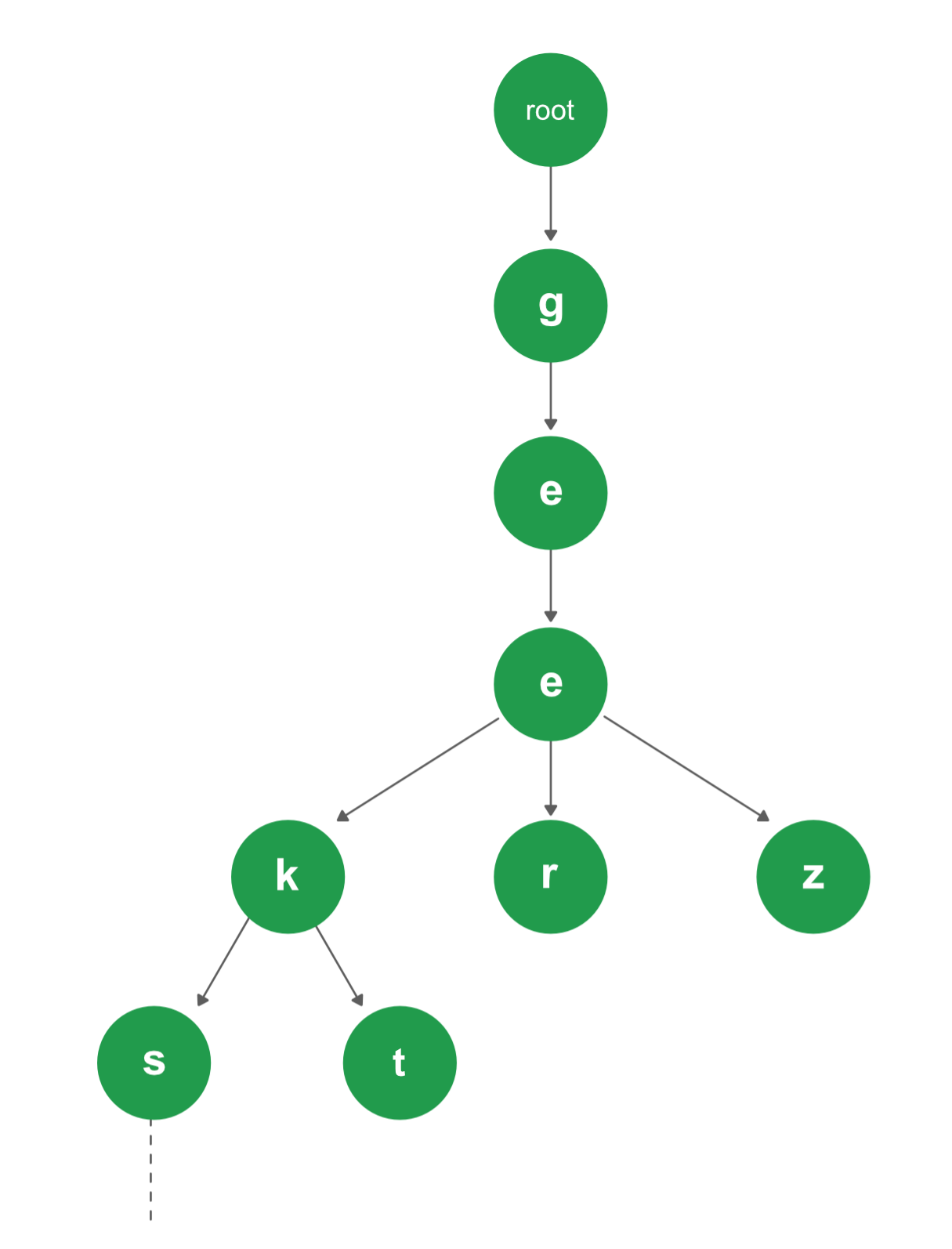
Every node of Trie consists of multiple branches. Each branch represents a possible character of keys. We need to mark the last node of every key as end of word node. A Trie node field isEndOfWord is used to distinguish the node as end of word node. A simple structure to represent nodes of the English alphabet can be as following,

// Trie node
struct TrieNode
{
     struct TrieNode *children[ALPHABET_SIZE];

     // isEndOfWord is true if the node
     // represents end of a word
     bool isEndOfWord;
};

Inserting

Inserting a key into Trie is a simple approach. Every character of the input key is inserted as an individual Trie node. Note that the children is an array of pointers (or references) to next level trie nodes. The key character acts as an index into the array children.

If the input key is new or an extension of the existing key, we need to construct non-existing nodes of the key, and mark end of the word for the last node.

If the input key is a prefix of the existing key in Trie, we simply mark the last node of the key as the end of a word.

The key length determines Trie depth.

Searching

Searching for a key is similar to insert operation, however, we only compare the characters and move down. The search can terminate due to the end of a string or lack of key in the trie. In the former case, if the isEndofWord field of the last node is true, then the key exists in the trie. In the second case, the search terminates without examining all the characters of the key, since the key is not present in the trie.

The following picture explains construction of trie using keys given in the example below,

                       root
                    /   \    \
                    t   a     b
                    |   |     |
                    h   n     y
                    |   |  \  |
                    e   s  y  e
                 /  |   |
                 i  r   w
                 |  |   |
                 r  e   e
                        |
                        r

In the picture, every character is of type trie_node_t. For example, the root is of type trie_node_t, and it’s children a, b and t are filled, all other nodes of root will be NULL. Similarly, “a” at the next level is having only one child (“n”), all other children are NULL. The leaf nodes are in blue.

Insert and search costs O(key_length), however the memory requirements of Trie is O(ALPHABET_SIZE * key_length * N) where N is number of keys in Trie. There are efficient representation of trie nodes (e.g. compressed trie, ternary search tree, etc.) to minimize memory requirements of trie.