zhihu 如何直观地解释 backpropagation 算法？

Anonymous的回答

BackPropagation算法是多层神经网络的训练中举足轻重的算法。

简单的理解，它的确就是**复合函数的微积分链式法则**，但其在实际运算中的意义比**链式法则**要大的多。

要回答题主这个问题“如何直观的解释back propagation算法？” 需要先直观理解**多层神经网络**的训练。

机器学习**可以看做是**数理统计**的一个应用，在**数理统计**中一个常见的任务就是**拟合，也就是给定一些样本点，用合适的曲线揭示这些样本点随着自变量的变化关系。

深度学习**同样也是为了这个目的，只不过此时，**样本点**不再限定为 $(x, y)$ 点对，而可以是由向量、矩阵等等组成的广义点对 $(X,Y)$ 。而此时， $(X,Y)$ 之间的关系也变得十分复杂，不太可能用一个简单函数表示。然而，人们发现可以用**多层神经网络**来表示这样的关系，而**多层神经网络**的本质就是一个**多层复合的函数。借用网上找到的一幅图[1]，来直观描绘一下这种复合关系。

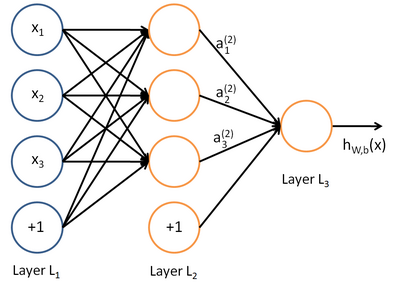
思考：这个图是存在错误的，图中 $a_1^{(2)}$ 其实应该画在圆圈中，而不是画在连线上。这其实是计算图。

其对应的表达式如下：

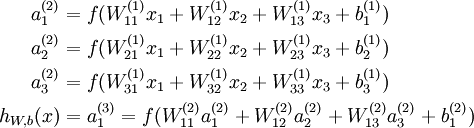
上面式中的 $W_{ij}$ 就是相邻两层神经元之间的权值，它们就是深度学习需要学习的**参数**，也就相当于直线拟合 $y=k*x+b$ 中的待求参数 $k$ 和 $b$ 。

和**直线拟合**一样，深度学习**的训练也有一个**目标函数，这个**目标函数**定义了什么样的参数才算一组“好参数”，不过在机器学习中，一般是采用**成本函数（cost function），然后，训练目标就是通过调整每一个权值 $W_{ij}$ 来使得**cost**达到最小。**cost函数**也可以看成是由所有待求权值 $W_{ij}$ 为自变量的**复合函数，而且基本上是非凸的，即含有许多**局部最小值**。但实际中发现，采用我们常用的**梯度下降法**就可以有效的求解最小化cost函数的问题。

梯度下降法需要给定一个初始点，并求出该点的**梯度向量**，然后以**负梯度方向**为搜索方向，以一定的**步长**进行搜索，从而确定下一个迭代点，再计算该新的梯度方向，如此重复直到cost收敛。那么如何计算梯度呢？

假设我们把**cost函数**表示为 $H(W_{11},W_{12}, \dots ,W_{ij}, \dots, W_{mn})$ , 那么它的梯度向量[2]就等于 $\nabla H = \frac{\partial H}{\partial W_{11} }\mathbf{e}_{11} + \cdots + \frac{\partial H}{\partial W_{mn} }\mathbf{e}_{mn}$ , 其中 $\mathbf{e}_{ij}$ 表示正交单位向量。为此，我们需求出cost函数H对每一个权值Wij的**偏导数**。而**BP算法正是用来求解这种多层复合函数的所有变量的偏导数的利器**。

我们以求 $e=(a+b)*(b+1)$ 的偏导[3]为例。它的复合关系画出图可以表示如下：

NOTE: $e=(a+b)*(b+1)$ 是一个二元函数，自变量为a，b，它可以看出是由两个函数复合而成： $c=a+b$ ，和 $d=b+1$

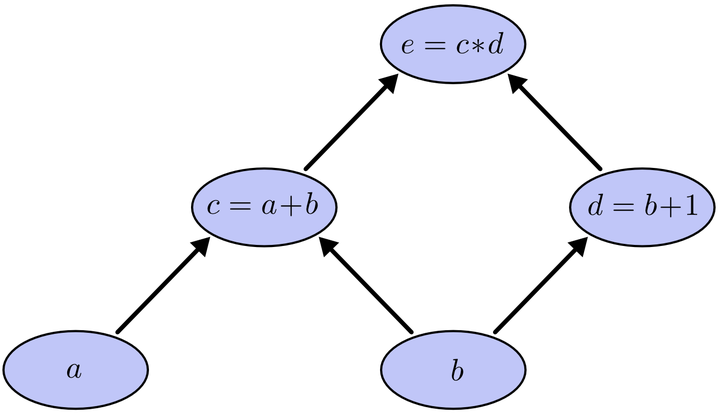
NOTE: 在machine learning中，需要使用结构化思维来思考函数，比如 $e=(a+b)*(b+1)$ ，上图就是它的图结构。这种图结构就是在6.5.1 Computational Graphs中描述的computational graph。

在图中，引入了中间变量 $c$ , $d$ 。为了求出 $a=2, b=1$ 时， $e$ 的梯度，我们可以先利用偏导数的定义求出不同层之间相邻节点的偏导关系，如下图所示。

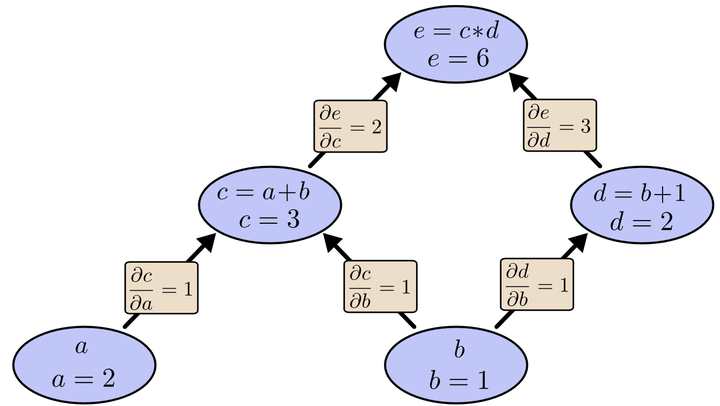
NOTE: 函数 $e=c*d$ ，当 $a=2,b=1$ ，则 $d=b+1=2$ ，则此时函数的表达式为 $e=2*c$ ，则 $e$ 对 $c$ 的导数为2（此时e的初始值为1，这在下面的段落中有交代）

利用链式法则我们知道：

$\frac{\partial e}{\partial a}=\frac{\partial e}{\partial c}\cdot \frac{\partial c}{\partial a}$ 以及 $\frac{\partial e}{\partial b}=\frac{\partial e}{\partial c}\cdot \frac{\partial c}{\partial b}+\frac{\partial e}{\partial d}\cdot \frac{\partial d}{\partial b}$ 。

链式法则在上图中的意义是什么呢？其实不难发现， $\frac{\partial e}{\partial a}$ 的值等于从a到e的路径上的偏导值的乘积，而 $\frac{\partial e}{\partial b}$ 的值等于从b到e的路径1(b-c-e)上的偏导值的乘积**加上**路径2(b-d-e)上的偏导值的乘积。

也就是说，对于上层节点p和下层节点q，要求得 $\frac{\partial p}{\partial q}$ ，需要找到从q节点到p节点的所有路径，并且对每条路径，求得该路径上的所有偏导数之乘积，然后将所有路径的 “乘积” 累加起来才能得到 $\frac{\partial p}{\partial q}$ 的值。

NOTE: chain rule和computational graph的对应关系。这种对应关系是非常巧妙的，它是backprop实现的关键所在：层与层之间是乘法关系，同层之间是相加关系；

大家也许已经注意到，这样做是十分冗余的，因为很多**路径被重复访问了**。比如上图中，a-c-e和b-c-e就都走了路径c-e。对于权值动则数万的深度模型中的神经网络，这样的冗余所导致的计算量是相当大的。

NOTE: 自底向上的方式进行计算，则肯定会导致冗余路径。

同样是利用链式法则，BP算法则机智地避开了这种冗余，它对于每一个路径只访问一次就能求顶点对所有下层节点的偏导值。

正如反向传播(BP)算法的名字说的那样，BP算法是**反向(自上往下)**来寻找路径的。

从最上层的节点e开始，初始值**为1，以层为单位进行处理。对于e的下一层的所有子节点，将1乘以e到某个节点路径上的**偏导值，并将结果“堆放”在该子节点中。等e所在的层按照这样传播完毕后，第二层的每一个节点都“堆放"些值，然后我们针对每个节点，把它里面所有“堆放”的值求和（因为这个节点是可能有多个proceeding node的），就得到了顶点e对该节点的偏导。然后将这些第二层的节点各自作为起始顶点，初始值**设为顶点e对它们的**偏导值，以"层"为单位重复上述传播过程，即可求出顶点e对每一层节点的偏导数。

以上图为例，**节点c**接受**e**发送的 $1*2$ 并堆放起来，**节点d**接受**e**发送的 $1*3$ 并堆放起来，至此第二层完毕，求出各节点总堆放量并继续向下一层发送。**节点c**向**a**发送 $2*1$ 并对堆放起来，**节点c**向**b**发送 $2*1$ 并堆放起来，**节点d**向**b**发送 $3*1$ 并堆放起来，至此第三层完毕，**节点a**堆放起来的量为2，**节点b**堆放起来的量为 $2*1+3*1=5$ , 即**顶点e**对**b**的偏导数为5.

举个不太恰当的例子，如果把上图中的箭头表示欠钱的关系，即c→e表示e欠c的钱。以a, b为例，直接计算e对它们俩的偏导相当于a, b各自去讨薪。a向c讨薪，c说e欠我钱，你向他要。于是a又跨过c去找e。b先向c讨薪，同样又转向e，b又向d讨薪，再次转向e。可以看到，追款之路，充满艰辛，而且还有重复，即a, b 都从c转向e。而BP算法就是主动还款。e把所欠之钱还给c，d。c，d收到钱，乐呵地把钱转发给了a，b，皆大欢喜。

【参考文献】 [1] 技术向：一文读懂卷积神经网络CNN [2] Gradient [3] http://colah.github.io/posts/2015-08-Backprop/ 其他推荐网页： \1. tensorflow.org 的页面 \2. Neural networks and deep learning

YE Y的回答

首先说这个图解的优点：先形象说明了**forward-propagation**，然后说明了**error backward-propagation**，最后根据**误差**和**梯度**更新权重。没错这是**backprop**，又非常直观，但是从前的backprop了。

backprop的发展路线大概是，1974年有个Harvard博士生Paul Werbos首次提出了backprop，不过没人理他，1986年Rumelhart和Hinton一起重新发现了backprop，并且有效训练了一些浅层网络，一下子开始有了名气。那个时候的backprop从现在看来并不是个很清晰的概念，把梯度和更新一块打包了，从这点看来和我贴出来的图是一回事。如果有看过mitchell机器学习教材的同学可能也会觉得下面的图眼熟。

随着神经网络的继续发展，到了深度学习大行其道的今天，更新权值的思路其实变得更简单粗暴了。概括一下就是，把原来打包式的做法拆开成了**1）求梯度**；2）梯度下降。所以现在我们再提到backprop，一般只是指第一步：求梯度。这就是为什么好多答案直接说就是个链式法则，因为确实就是链式法则。

不过个人觉得还是有可以直观理解的一些点：

1）链式法则的直观理解的，之所以可以链式法则，是因为梯度直观上理解就是一阶近似，所以梯度可以理解成某个变量或某个中间变量**对输出影响的敏感度的系数**，这种理解在一维情况下的直观帮助可能并不是很大，但是到了高维情况，当**链式法则**从乘法变成了**Jacobian矩阵乘法**的时候，这个理解起来就形象多了。神经网络中的链式法则恰好都几乎是高维的。

2）Computational graph。最高票答案和 @龚禹pangolulu 的答案中都有提到，就不赘述，其实就是**计算代数**中的一个最基础办法，从计算机的角度来看还有点**动态规划**的意思。其优点是表达式给定的情况下对**复合函数**中所有变量进行**快速求导**，这正好是神经网络尤其是深度学习的场景。现在主流深度学习框架里的求导也都是基于Computational Graph，比如theano，torch和tensorflow，Caffe也可以看做是computaiona graph，只不过node是layer。

总结：图中的确实是backprop，但不是深度学习中的backprop，不过backward的大体思想是一样的，毕竟误差没法从前往后计算啊。

以下是原回答：

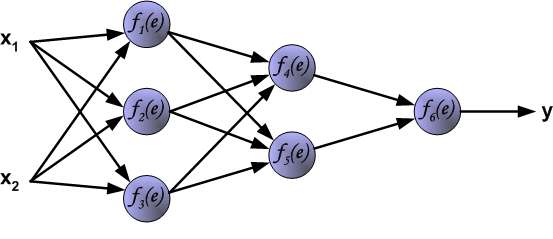
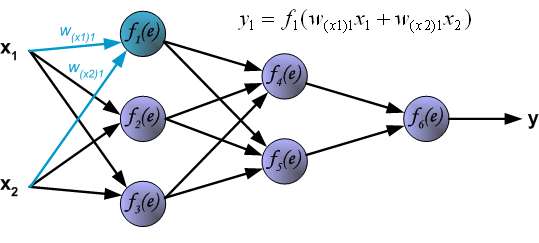
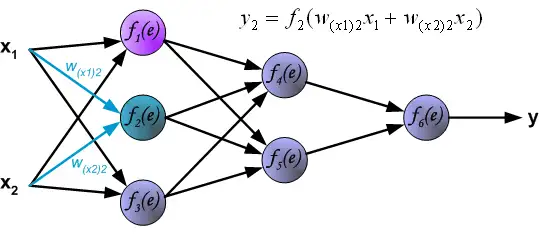
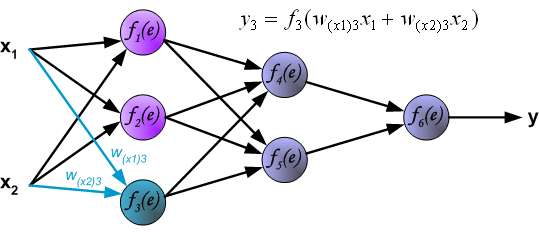
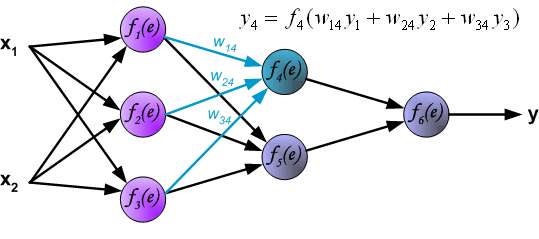
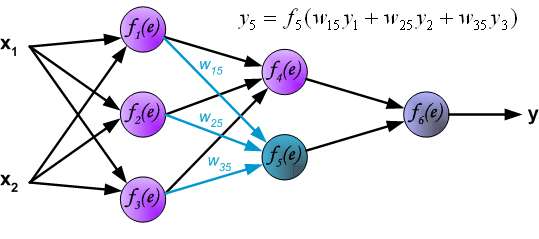
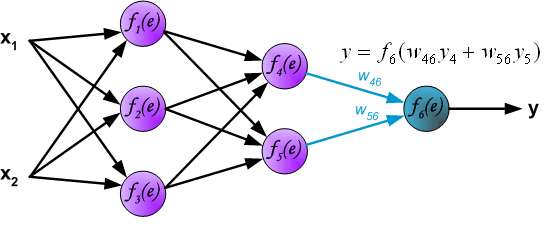
In the next algorithm step the output signal of the network y is compared with the desired output value (the target), which is found in training data set. The difference is called error signal $\delta$ of output layer neuron.

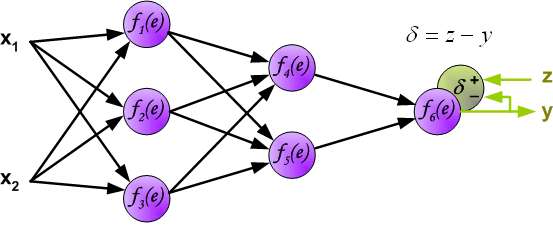
It is impossible to compute error signal for internal neurons directly, because output values of these neurons are unknown. For many years the effective method for training multiplayer networks has been unknown. Only in the middle eighties the backpropagation algorithm has been worked out. The idea is to propagate error signal d (computed in single teaching step) back to all neurons, which output signals were input for discussed neuron.

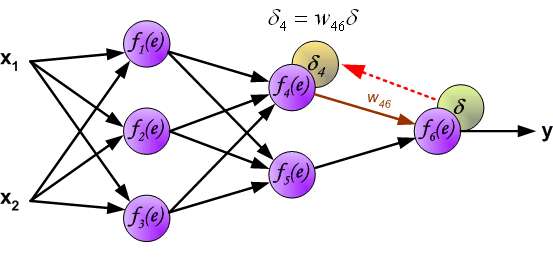
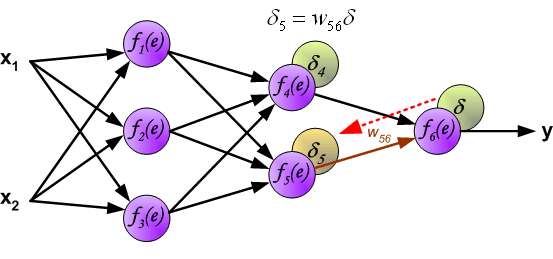
The weights' coefficients $w_{mn}$ used to propagate errors back are equal to this used during computing output value. Only the direction of data flow is changed (signals are propagated from output to inputs one after the other). This technique is used for all network layers. If propagated errors came from few neurons they are added. The illustration is below:

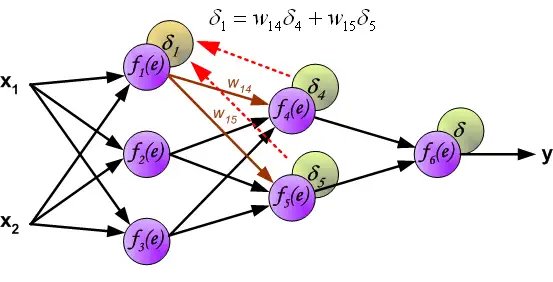
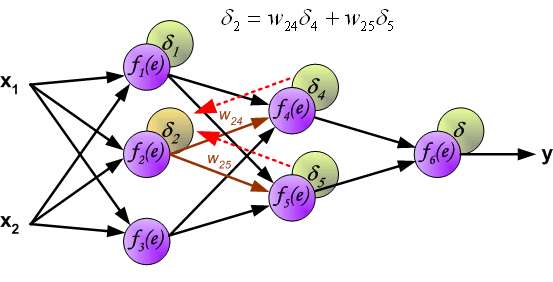
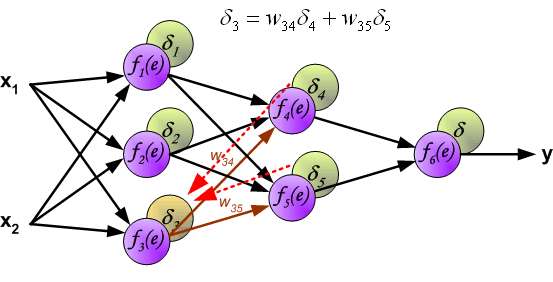
When the error signal for each neuron is computed, the weights coefficients of each neuron input node may be modified. In formulas below df(e)/de represents derivative of neuron activation function (which weights are modified).

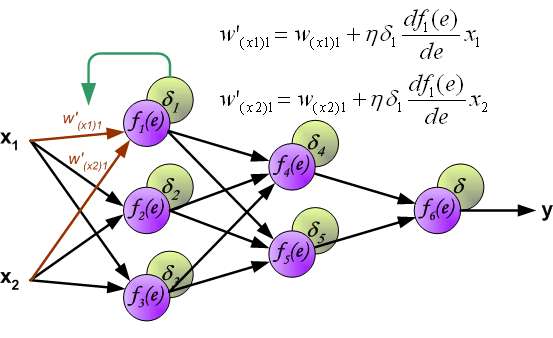
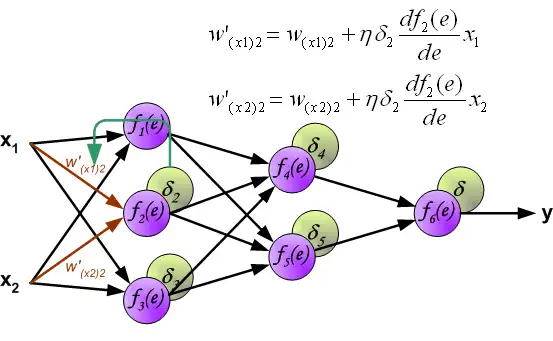
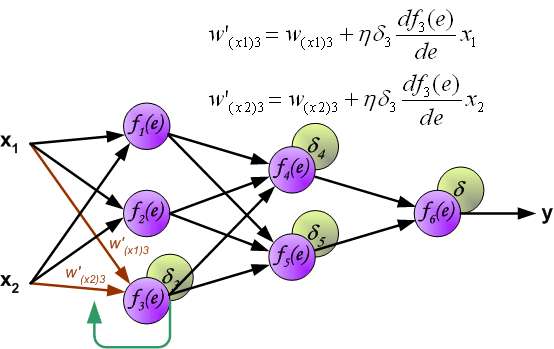
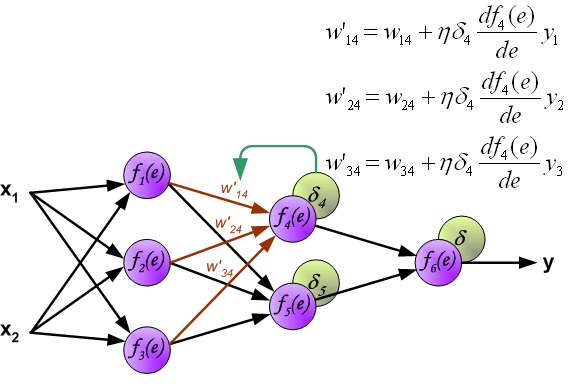
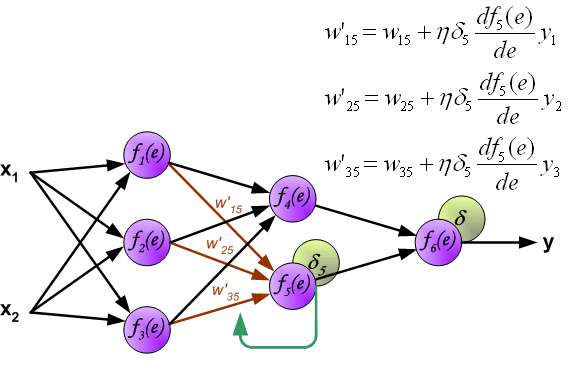
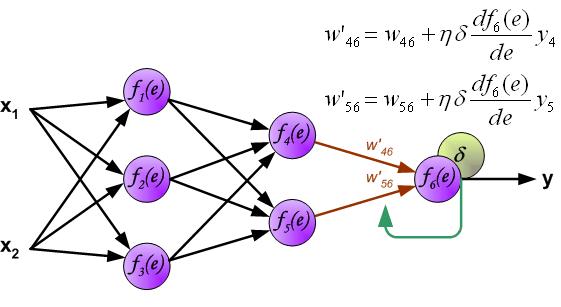
Coefficient $\eta$ affects network teaching speed. There are a few techniques to select this parameter.

The first method is to start teaching process with large value of the parameter. While weights coefficients are being established the parameter is being decreased gradually.

The second, more complicated, method starts teaching with small parameter value. During the teaching process the parameter is being increased when the teaching is advanced and then decreased again in the final stage. Starting teaching process with low parameter value enables to determine weights coefficients signs.

References Ryszard Tadeusiewcz "Sieci neuronowe", Kraków 1992

http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html