Skip to content

递归函数的表示与分析

1、下面总结了表示递归函数执行过程的表示方法。

2、有了前面章节的理论基础，理解本章的内容是非常简单的

3、这个问题，其实转换为了Represent-describe-tree

递归调用树

对递归函数进行复杂度分析是非常重要的，因为所有使用递归的函数都涉及这个问题；其实复杂度分析本质上来说是统计递归函数的执行次数、执行深度等问题，所以如果对递归函数的调用过程有一个直观，准确地描述的话，那么分析其递归函数的复杂度也会非常容易，目前流行的表示方法是：递归调用树，如下是一些使用递归调用树来表示：

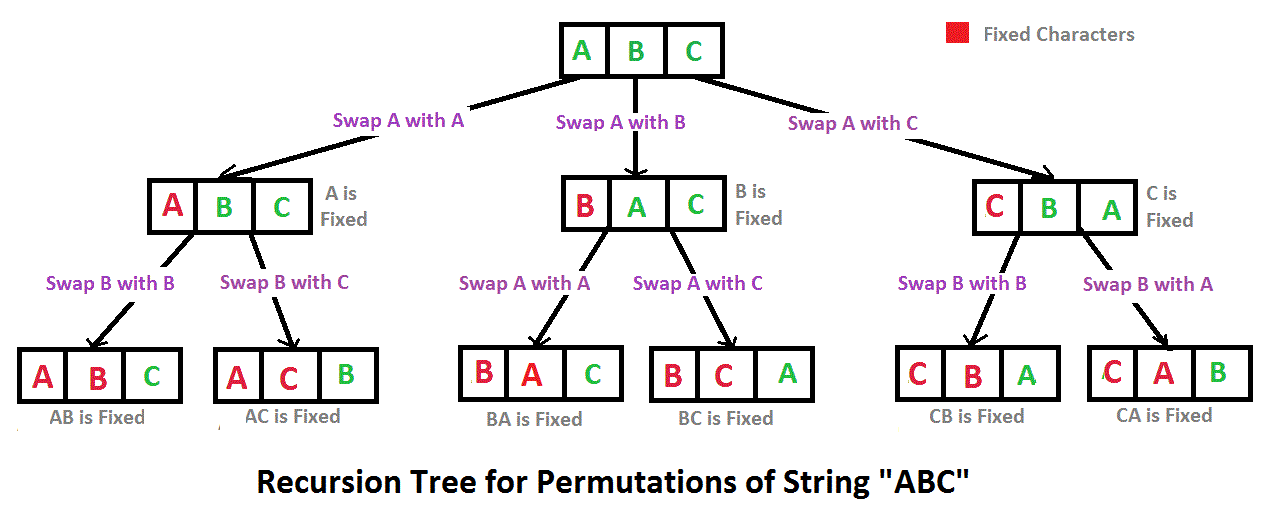
geeksforgeeks Write a program to print all permutations of a given string

NewPermutation

leetcode 斐波那契数

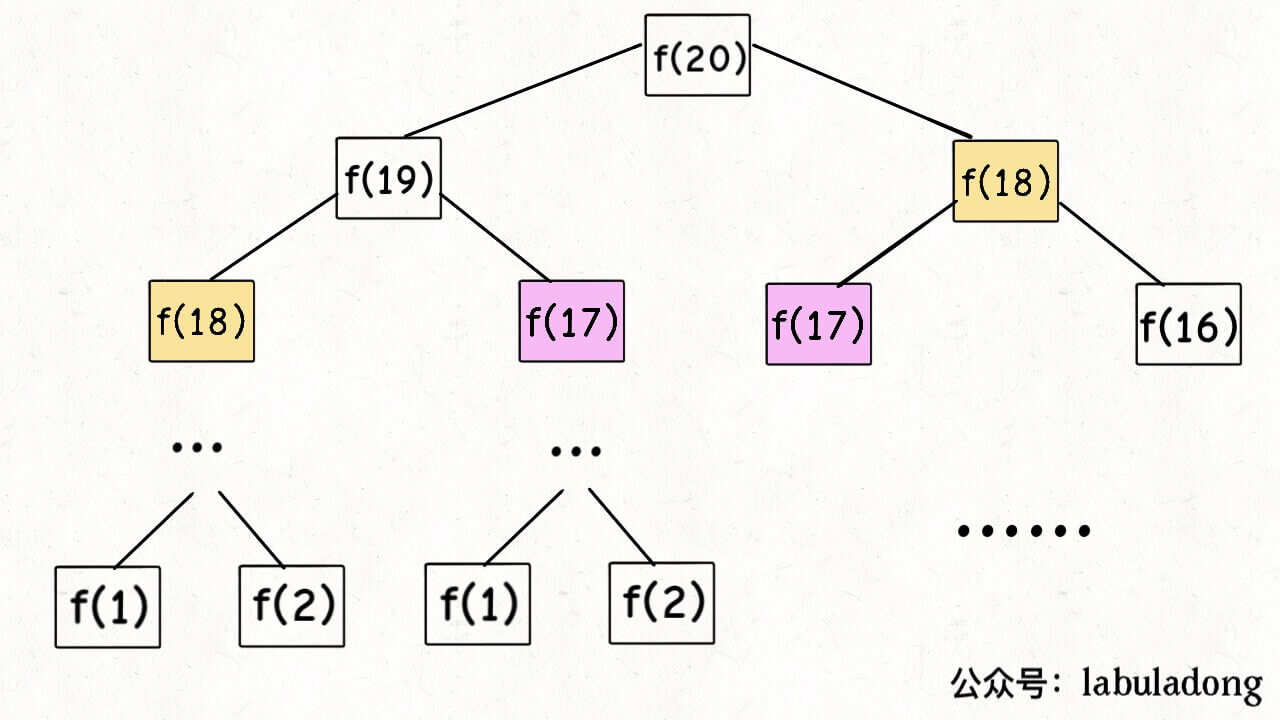
fibtree

那如何来理解**递归调用树**呢？实际上，递归函数**的执行过程并不会显示的构造出一个**递归调用树，它只是逻辑上形成了一个树，下面对此进行详细的分析：

我们知道，函数的调用过程所使用的是Call stack，每一次的函数调用都会在Call stack上push一个 stack frame（参见Call stack）；递归函数一直执行的是同一个函数，所以它的Call stack中的**stack frame**的执行逻辑是相同的（入参可能不同）；在递归函数执行的过程中，每执行一次递归调用就往Call stack上push（入栈）一个 stack frame，直到某个递归函数执行到了base case，则它会return，这就意味中它的 **stack frame**会pop（出栈），则控制会返回到调用它的函数；显然，前面所描述的过程对应这树的深度优先遍历，所以我们说：递归函数的执行过程是对递归调用树进行深度优先遍历。

NOTE: 上面所描述的：函数调用-入栈，函数返回-出栈，非常类似于括号匹配算法中的正括号入栈，反括号出栈；

总的来说，递归调用数是对递归函数的Call stack的可视化分析；

其实我们是完全可以根据**递归函数**画出对应的**递归调用树**的。比如perm函数就是典型的**排列树**，二分搜索、quike sort等就是典型的**二叉树**。

geeksforgeeks Matrix Chain Multiplication | DP-8

MatrixChain

使用括号表示

在 wikipedia Recursion (computer science) # Recursive programs 中给出了使用括号来表示recursive function execution的例子。

Factorial

\operatorname {fact} (n)={\begin{cases}1&{\mbox{if }}n=0\\n\cdot \operatorname {fact} (n-1)&{\mbox{if }}n>0\\\end{cases}}

Computing the recurrence relation for n = 4:

b4       = 4 * b3         
         = 4 * (3 * b2)
         = 4 * (3 * (2 * b1))
         = 4 * (3 * (2 * (1 * b0)))
         = 4 * (3 * (2 * (1 * 1)))
         = 4 * (3 * (2 * 1))
         = 4 * (3 * 2)
         = 4 * 6
         = 24

Towers of Hanoi

Main article: Towers of Hanoi

$$ \operatorname {hanoi} (n)={\begin{cases}1&{\mbox{if }}n=1\2\cdot \operatorname {hanoi} (n-1)+1&{\mbox{if }}n>1\\end{cases}} $$ Computing the recurrence relation for n = 4:

hanoi(4)     = 2*hanoi(3) + 1
             = 2*(2*hanoi(2) + 1) + 1
             = 2*(2*(2*hanoi(1) + 1) + 1) + 1
             = 2*(2*(2*1 + 1) + 1) + 1
             = 2*(2*(3) + 1) + 1
             = 2*(7) + 1
             = 15

递归函数的复杂性分析

geeksforgeeks Analysis of Algorithm | Set 4 (Solving Recurrences)